阿摩線上測驗
39 假設{X1, X2,....., X n } 是一抽自常態母體的「隨機樣本」，若 µ 代表母體平均數，而且母體標準差已知
為 1。今欲檢定 H0：μ＝10 相對於 H1：μ＞10。若要求「型Ⅰ錯誤」機率α＝16 %而且在μ＝11.5
時之「型Ⅱ錯誤」機率β＝2.5 %，則所需樣本數 n 為何？（根據 P(|Z|＞ 2) ≈ 5 %，P(|Z|＞ 1) ≈ 32 %，其
中 Z 具有「標準常態分配」）
(A) 4
(B) 9
(C) 16
(D) 25
答案：登入後查看
統計： A(34), B(13), C(23), D(6), E(1) #146526
統計： A(34), B(13), C(23), D(6), E(1) #146526
詳解 (共 4 筆)
mej58763
#6222337
先寫已知條件,H0:u=10,H1:u>10,alpha=0.16,當u=11.5,beta=0.025
alpha=0.16=P(X平均值>某個值當u=10)=P(Z>(x-10)/(1/sqrt(n))=P(Z>1)
x-10=1/sqrt(n)
beta=0.025=P(X平均值<某個值當u=11.5)=P(Z<(x-11.5)/(1/sqrt(n)))=P(Z<-2)
x-11.5=-2/sqrt(n)
ㅤㅤ
解聯立,-2*x+10*2=x-11.5.x=10.5,10.5-10=1/sqrt(n),0.5=1/sqrt(n),n=4
0
0
Hsu Lingling
#4601359
怎麼算呢？
0
0
Chris Wang
#532345
這題考好冷門的公式阿
0
0
Miho16
#7209655
根據題意
α＝16%
β＝2.5%
β＝2.5%
Zα＝1
Zβ＝2
Zβ＝2
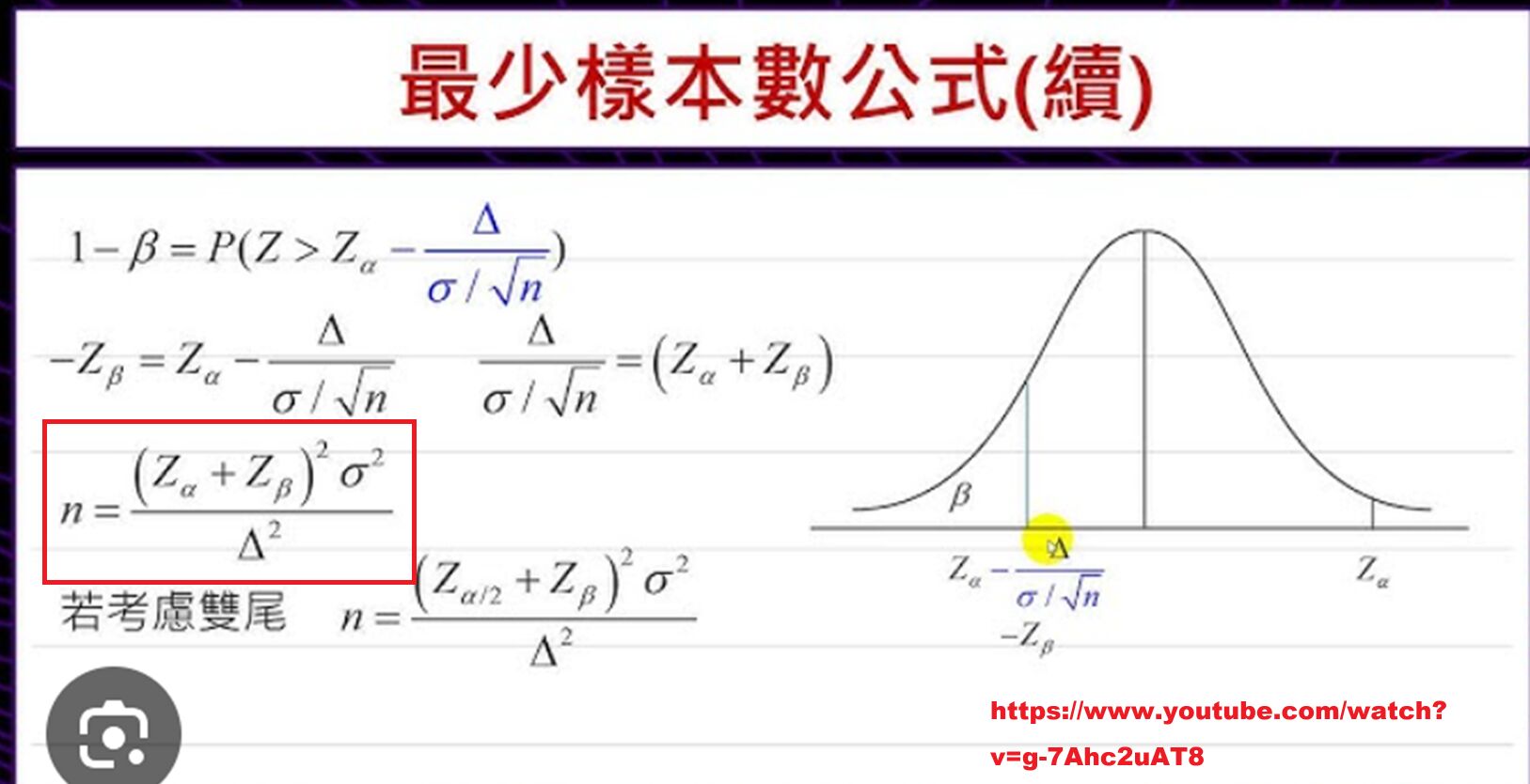
代入公式可得
n=(1+2)^2*1^2/(11.5-10)^2=4
0
0