四、圖三所示之電路中,試求: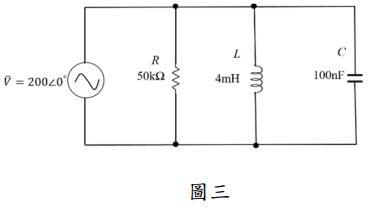
題目資訊:
計算品質因數 (Q):
對於理想的並聯 RLC 電路(電阻、電感、電容直接並聯),品質因數 Q 的計算公式為:
Q=RLC
現在我們將已知的數值代入公式:
代入數值: Q=(50×103Ω)×4×10−3H1×10−7F
計算根號內的部分: LC=4×10−31×10−7=41×10−7−(−3)=0.25×10−4
開根號: 0.25×10−4=(0.5×10−2)2=0.5×10−2
計算最終 Q 值: Q=(50×103)×(0.5×10−2) Q=(50×0.5)×103+(−2) Q=25×101 Q=250
其他計算方式 (驗證用):
也可以先計算諧振頻率 ω0,再用其他 Q 的公式計算。
 1=(4×10−3)×(1×10−7)1=4×10−10
1=(4×10−3)×(1×10−7)1=4×10−10 1=2×10−51=0.5×105=5×104rad/s
1=2×10−51=0.5×105=5×104rad/s答案:
該電路的品質因數 Q 為 250。