申論題 - 阿摩線上測驗

申論題資訊

試卷：104年 - 104 國立交通大學_碩士班考試入學試題_資訊聯招：線性代數與離散數學#113284
科目：交大◆資工◆線性代數與離散數學
年份：104年
排序：0

題組內容

5. Let A be an m x n matrix, X∈Rⁿdenote a vector, and L(x) = Ax be a linear transformation. row(A), col(A), and N(A) respectively represent the row space, the column space, and the null space of A. rank(A) and nullity(A) respectively represent the rank and nullity of A. kernel(L) and range(L) respectively represent the kernel and the range of L. If V is a vector space/subspace, dim(V) denotes the dimension of V.Consider the following statements:

(A) row(A) = Rⁿ.

(B) col(A) = R^m.

(C) dim(col(A)) ＜m.

(D) Ax = 0 has infinite solutions.

(E) Ax = 0 has exactly one solution.

(F) Ax = 0 has no solutions.

(G) Ax = 0 is an inconsistent system.

(H) Ax = 0 is a consistent system.

(I)N(A)=⌀.

(J) rank(A) =m.

(K) nullity(A) = m.

(L) kernel(L) = Rⁿ.

(M)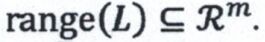

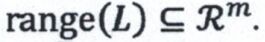
(N) AA^T is not symmetric.

申論題內容

(c) (2 points) Which statements are equivalent to the statement (B)?