申論題

一、
 一九二八年，約翰．馮．諾曼感於當時的經濟學理論不足，於是運用了比賽中雙方皆想要取勝的心理，希望透過理性分析「賽局」的方式，進而思考人類的決策行為，這就是著名的賽局理論（game theory）。
 從最簡單的時間規劃、球類競賽與人際互動，都可以利用賽局理論進行決策。例如：放學後，是和同學一起練習發表簡報，還是準備明天的數學測驗？與好朋友出去看電影，是選擇浪漫電影，還是動漫電影？
 而賽局理論就能幫助陷在選擇情境的人做出最佳的決策。它不只思考構成「賽局」的要素是什麼，並將每位決策者對其他決策者行為的了解和預期納入考量，使人能清晰地看出雙方的選擇及對彼此的影響。這有助於預測局勢的得失，從而制定出牽制對手、最終取勝的策略。在賽局裡，每位決策者都會想以最優、最利己的策略來回應對方的戰略，結果在攻防拉鋸中，兩者最終會選擇使雙方損、利達成一致的情況，最經典的例子就是「囚徒困境」。
 以一個證據不足的犯罪事件為例，有兩名共犯被捉，他們被分開審訊，完全沒有串供的機會。這時，檢察官給他們各自選擇的條件：如果兩人都不認罪，將各判一年徒刑；如果一人認罪而另一人不認罪，認罪者成為汙點證人免除刑責，不認罪者將被判五年徒刑；若兩人都認罪，則各被判三年徒刑。
 依據賽局理論，我們可以用一個簡單的矩陣結構來分析：
 
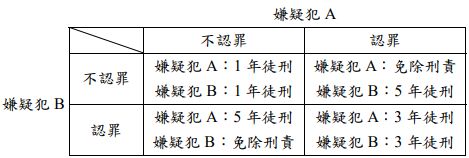
 兩名嫌犯都希望自己能免除刑責，但因為分開審訊的緣故，讓他們心中的盤算：除了考量自己最有利的刑責之外，也不得不揣測對方的選擇。於是他們最終都選擇認罪，而各自被判三年徒刑，這樣的平衡，就是「囚徒困境」。
                                             （參考資料：徐渭文《策略的藝術：培養贏家邏輯，從賽局思考開始！》、
                                                 巫和懋、夏珍《賽局高手――全方位策略與應用》）
請分項回答下列問題：

問題 (二)：
舉出生活中實際例子來印證賽局理論所說的困境，並對事例中的困境提出自己的解方或看法。文長限 400 字以內（至多 19 行）。（占 21 分）