三、在控制兩個方向的區集效應時，經常由於試區受限，無法達到拉丁方格的設計，此時可以變通成 為列與行的設計（row-and-column design） 。下列的試驗設計與數據摘自於 Pearce 所著之「作物試 驗手冊」 Manual of crop experimentation）
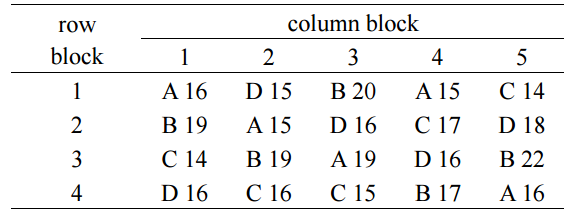
表中顯示：處理數為 4 並以代號 A, B, C, D 表示，橫向區集數為 4，直向區集數為 5。經統計計 算軟體計算結果顯示如下，下列為第一型平方和（Type I SS）
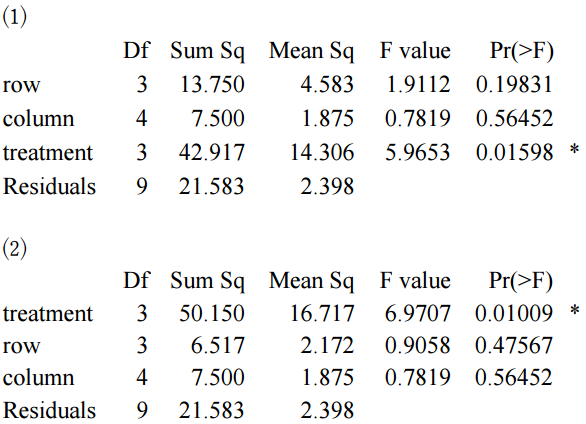
上面兩個變方分析表的差別為變因的順序不同，在表1. treatment 處理的順序為 3，但是在表2.其 順序則為 1。隨著順序的改變，其所對應的平方和也不同，這顯示「處理」與「列區集」兩者間 的非直交性。此設計所對應之模式為
Yij ( k ) = µ + ri + c j + τ ( k ) + ∈ij
i = 1,2,3,4 ；1,2,3,4,5； k = 1,2,3,4
上述的模式用於表示兩個方向的資料，所以使用兩個下標 i, j 就足夠了， 「處理」的下標 k 事實上 當 i, j 決定後即固定下來，例如當 i = 1, j = 2 時 k = 4 （處理為 D） 。請回答下列問題：
阿摩線上測驗
登入