題組內容

第三題： 一個數值在儲存到電腦記憶體內部之前，會先被轉換成二進位系統。一個數值使用定點法(fixed-point)表示儲存成一個整數，另外，以浮點法(floating-point)表示將一個數值儲存成一個實數。請回答下列問題：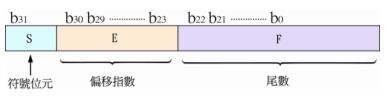
667a8a122ee11.jpg
 (一)一個整數儲存在記憶體中通常是使用定點法表示，其中，2 補數(2’s complement) 是常在計算機科學中用來儲存一個 n 位元記憶體位置的有號(Signed)整數。請問：

3.運用 2 補數系統的數字加法，請詳述兩個整數『–28』、『33』相加的運算過程， 以及運算結果。【6 分】

詳解 (共 1 筆)

詳解 提供者：Aaron Lim
  1. 首先,我們需要將這兩個數字轉換為2補數表示。假設我們使用8位元系統。
  2. 對於 -28: a) 28的二進制是: 00011100 b) 取反: 11100011 c) 加1: 11100100 所以 -28 的2補數表示是: 11100100
  3. 對於 33: 33的二進制就是: 00100001
  4. 現在我們將這兩個數相加: 11100100 (-28)
    • 00100001 (33) ———————————— 100000101
  5. 結果分析:
    • 我們得到了9位元的結果,但因為我們使用的是8位元系統,所以最高位的進位會被忽略。
    • 忽略進位後的結果是: 00000101
  6. 將 00000101 轉換回十進制: 02^7 + 02^6 + 02^5 + 02^4 + 02^3 + 12^2 + 02^1 + 12^0 = 4 + 1 = 5

因此,在8位元2補數系統中,-28 + 33 的結果是 5,這與實際的數學運算結果相符。

這個過程展示了2補數系統的一個優點:我們可以用相同的加法運算來處理正數和負數的加法,不需要特別的減法電路。

需要注意的是,如果結果超出了8位元系統的表示範圍(-128 到 127),就會發生溢出。在這個例子中,結果在範圍內,所以沒有發生溢出問題。