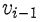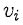4. Let G be a simple graph. A path of G is a sequence of distinct vertices v0,v1, Uh such that and are adjacent for each i = 1,2,..., k. The length of the path v0, v1 , ..., is k. The degree of a vertex is the number of edges incident to that vertex. Show that if the minimum degree of G is greater than or equal to k, then G has a path whose length is at least k.