題組內容

二、X 為前測成績，Y 為後測成績。假設甲乙兩班的前、後測成績關係分別為

甲： Y =β₀₁ + β₁₁X+ ε

乙： Y= β₀₂+ β₁₂ X + ε

下表資料中 G 代表班別（G = 1 為甲班，G = 0 為乙班），令 XG 為 X 和 G 乘積。

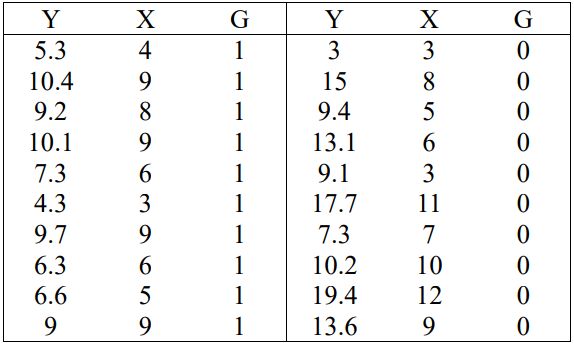
我們以上表資料分別配適以下四組迴歸：M1：Y 對 X 迴歸；M2：Y 對 G 迴歸；M3：Y 對 X 和 G 複迴歸；M4：Y 對 X、G 和 XG 複迴歸。變異數分析結果如下：

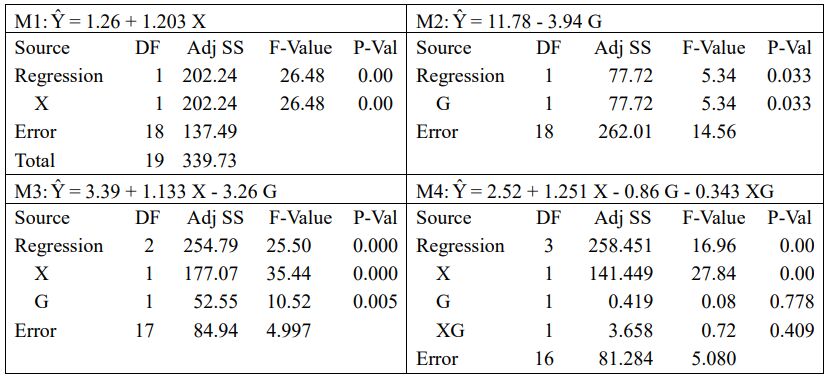
在顯著水準 0.05 下，試求：

(二)檢定「兩班是否有相同之 Y 對 X 線性關係（相同的斜率及截距）」，即 H₀：β₁₁ β=₁₂ and β₀₁=β₀₂ vs. H₁：H₀ 為非。（15 分）