題組內容

7.教師在高年級數學課室的教學活動：在一個不等邊銳角三角形中，請學童以其中一邊為長或寬，畫出一個包住此三角形的長方形，且三角形的另一個頂點落在長方形的邊上。有三位學童畫出三個不同的圖形如下：教師問學童：「這三個長方形的面積是否相等？」某學童回答：「不相等，丙圖的面積最大。」試回答下列問題：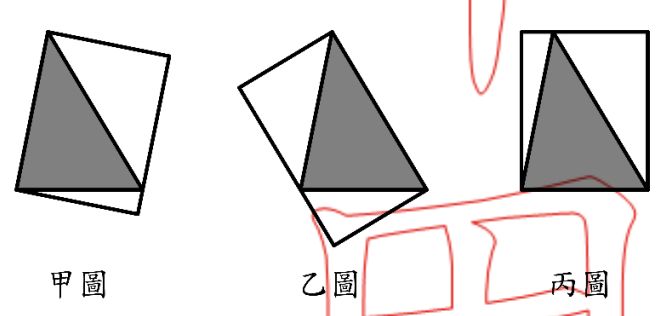

(2)請用國小學童可以理解的方式，說明這三個長方形面積的關係。【3 分】

詳解提供者：阿貴

證明三個長方形皆為三角形的一半，因三角形皆相同，因此長方形都一樣。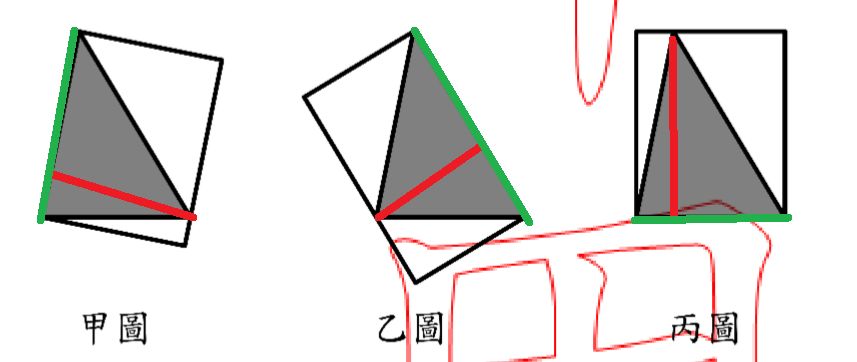

因為，從圖可知，

甲/乙/丙三角形的底=甲/乙/丙長方形的長

甲/乙/丙三角形的高=甲/乙/丙長方形的寬

又三角形面積=底*高/2

長方形面積=長*寬

因此可知甲/乙/丙三角形面積/2=甲/乙/丙長方形面積

又甲乙丙三角形相同，因此甲乙丙長方形面積相同

詳解提供者：chunchun0515dreaming

甲圖的三角形面積:底(長方形的長)x高(長方形的寬)/2 乙圖的三角形面積:底(長方形的長)x高(長方形的寬)/2 丙圖的三角形面積:底(長方形的寬)x高(長方形的長)/2 三個圖的三角形面積都是由相同的數相乘,所以得到面積大小也會是相同的

詳解提供者：Sherry Cheng

可將三角形依照每個底畫出高，便可將灰色部分分成兩個三角形，長方形也變成兩個長方形，便會發現灰色的兩塊三角形分別為兩塊長方形的一半，即可得知長方形為此灰色的三角形的2倍。

詳解提供者：Ying-Tong Guo

底和高相乘答案一樣所以面積一樣乘法交換率

詳解提供者：臺中音樂榜首

劃出所有三角形的高與底，代入三角形面積公式，底乘以高除以二後，可證實這三個三角形等高等底，故面積相等。

詳解提供者：神奇的蛞蝓

我的話會將三角形的面積算法做延伸為解答。三角形面積為低*高÷2，長方形的面積為長*寬，這3個長方形都是用同一個三角形去畫出來的所以面積只要把原本的三角形*2就好，所以三個長方形一樣大。

詳解提供者：YAMI

(繪製輔助線,將圖形分割為四個直角三角形說明)

詳解提供者：黃唯嘎

剛好是三角形的兩倍

詳解提供者：C-Y-C

分割為四個直角三角形說明

詳解提供者：sj920327

這三個長方形的面積關係是相等的。

以下是可以用國小學童理解的方式說明的理由：