申論題

(6) (25%) Consider a discrete memoryless source (DMS) with the associated source alphabet X := {a, b, c, d, e,f, g}. Each source output is independenty selocted from C with the probability distribution Px given in Table 1. The goal of source coding for the DMS is to construct a code C that assigns cach symbol 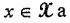bit string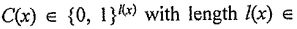N. Its average length is defined as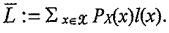Moreover, the code is usually required to be uniquely decodable.  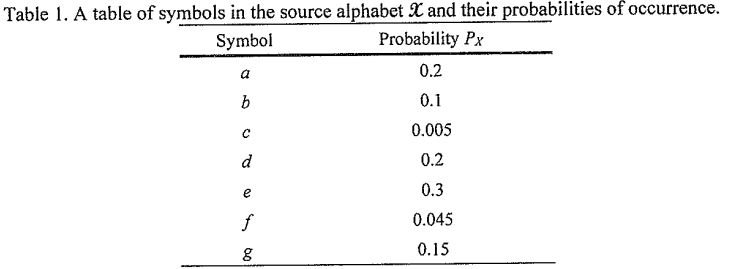 Please answer the following questions.

(b) (5%) A class of codes called the prefix-free codes can be decoded with no delay (hence sometimes also called instantareous codes). What is the definition for the prefix-free codes?
 Every prefix-free code for the alphabet 9X with its codeword lengths must satisfy the Kraftinequality. What is the Kraft inequality?
Assume that a code with its codeword lengths satisfies the Kraft inequality. Is it uniquely decodable? Does a uniquely decodable code have to satisfy the Kraft inequality?