申論題

4. (Total-18%) Consider a binary symmetric channel with input X, output Y, and transition probability a. More specifically, as shown in the figure below, the input and output of the channel may be "0" or "1", P(Y=0|X=0)= P(Y = 1|X = 1) = 1 - a and P(Y = 1|X = 0) = P(Y=0|X=0) = a. The prior probability is P(X = 0) = p.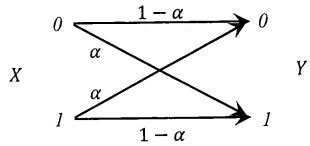

(d) (5%) Suppose the prior probability is not known in advance. We manage to produce an estimated prior probability  which may or may not be equal to the true prior probability P(X = 0) = p. In this case, the cross- entropy between the true and estimated prior distributions P and is defined by , which can be considered as an approximated entropy of X. Please show that the cross- entropy is always no less than the true entropy H(X) of X, i.e. 
 (Hint: You may use the Jensen's inequality: plog₂ a + (1 -p)log₂≤ b ＜ log₂(pa +(1 -p)b) for 0 ≤p ≤ 1, a ＞ 0, and b ＞0.)