申論題

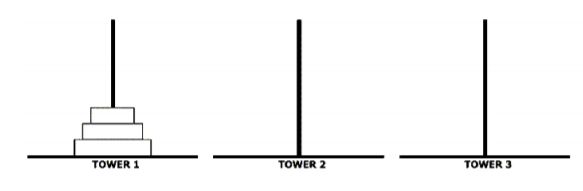
第三題： 河內塔(The Tower of Hanoi)是由艾德華．盧卡斯(É douard Lucas)在 1883 年提出的一個 數學遊戲，至今已經超過一百年歷史。河內塔由三根柱子和許多不同大小的圓盤組成。這個 難題從一個整齊堆疊在一根柱子上的圓盤開始。首先在一根柱子上，所有的圓盤按照大小的 順序，由下而上，依照大到小的順序放置在此根柱子上（最小的在頂部，最大的在底部）。 這個遊戲的目的是將所有的圓盤移動到另一根柱子上。但移動過程必須遵循以下規則：                                                                                                                         ● 一次只能移動一個圓盤。                                                                                                                             ●  每次只有放在柱子最上層的那個圓盤可以被移動。                                                                                  ●  任何時候，大的圓盤不能疊在小的圓盤上面，也就是圓盤必須由下而上，依照大到 小的順序放置。          ● 最終所有圓盤依照此規則，移到另一根柱子上。

（三）遞迴關係(recurrence relation)，是一種遞迴地定義一個序列的方程式：序列的每 一項目定義為前面一項或多項的函數。例如序列 1,2,3,5,8,13,21,34,55,….。若用 a(n)表示第 n 項的值。此序列的第一項為 a(1)=1, 第二項 a(2)=2，第三項則為 a(3)=a(2)+a(1)。依此類推，當 n＞2 時，第 n 項為 a(n)=a(n-1)+a(n-2)。此為序列 a(n)的遞迴關係。不同序列，可能會有不同的遞迴關係式。 回到我們的河內塔遊戲。假設有 n 個圓盤依序堆疊在柱子 1，將其移動到柱子 3 需要移動最少 f(n)次。則 n-1 個圓盤就需移動最少 f(n-1)次。依此類推。請找出 f(n) 和 f(n-1)及/或 f(n-2), … f(2), f(1)的遞迴關係。並請解釋你所找出的關係。【10 分】