Let Y be the vector space of 2x2 mattices with real entries, and P3 the vector space of real polynomials of dogree 3 or less. Detine the linear transformation T: V → P3 by 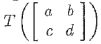 == 2a+(6-d)t-(a+c)x2+(a+6-c-d)x3. Find the rank and nullity of T.
== 2a+(6-d)t-(a+c)x2+(a+6-c-d)x3. Find the rank and nullity of T.
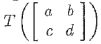 == 2a+(6-d)t-(a+c)x2+(a+6-c-d)x3.
== 2a+(6-d)t-(a+c)x2+(a+6-c-d)x3.