110年 - 110 國立中央大學_碩士班招生考試_數學系/數學、應用數學組(一般生、在職生):線性代數#105306

選擇題 (0)

申論題 (10)

a. (5pts) Find the reduced row echelon form of its augmented matrix (A|b).

b. (10pts) Explicitly find the solution set K of this linear system, including a particular solution and a basis for its homogeneous solution set K_H.

2. (15pts) Consider the following matrix
Find a diagonal matrix D and an invertible matrix Q such that If it is impossible, give a convincing reason.

a. (5pts) Find the characteristic polynomial of T.

b. (5pts) Find the minimal polynomial m(x) of T. Explain why your answer is indeed

minimal.
Hint: by defnition, m(x) is the monic non-zero polynomial with smallest degree such that m(T) is the zero map onR⁴.

4. (10pts) Let V = C³ be equipped with the standard inner product ＜, ＞. Let f: V → C be the unique linear map defined by

In other words, f is an element in V*. Find the unique vector z V such that

5. (15pts) Let W be the subspace of R⁴spanned by the following vectors

ข₁=(1,-1,0,0) ข₂=(0,1,-1,0) ข₃=(0,0,1,-1)

Apply the Gram-Schmidt algorithm to obtained an orthogonal basis for W.

6. (15pts) Let V be a fnite dimensional vector space over C. Let T : V →Vbe a linear map and

let W be an T-invariant subspace of V. Suppose that U₁, U₂, , U_nare eigenvectors in V of T

corresponding to distinct eigenvalues λ₁, λ₂, , λ_n in C. Prove that if u₁ +u₂+...+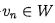

then. (Hint: induction on n)

7. (10pts) Let V = Rⁿbe equipped with the standard inner product ＜, ＞. Suppose that is a set of non-zero orthogonal vectors in V (m≤ n). Show that S is linearly independent.

8. (10pts) Let V and W be finite dimensional vector spaces and let T : V→ W be a linear map. Recall that there exists a unique linear map T^t : W*→ V*, called the transpose of T, where V* and W* are the dual spaces of V and W, respectively.
Consider V = R²and W = R³. Let T : V → W be the linear map defined by

T(a,b)=(3a+6,a-26,2a-6)

Then there exists a unique linear map T^t : W* →V* as above. Define

Hint: you need to either explicitly write down T^t(θ)(a,b) for any (a,b)

, or simply write down a 2 x 1 matris representing T^t(θ).

110年 - 110 國立中央大學_碩士班招生考試_數學系/數學、應用數學組(一般生、在職生):線性代數#105306

試卷資訊

選擇題 (0)

申論題 (10)