申論題

3. (20%) Consider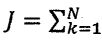Y to be a compound Poisson distribution, where N follows a Poisson distribution with the expected number of event occurrences to be λ, and for each event occurrence, one receives a payoff Y, which follows an independent and identical normal distribution, ie., Y~ND(μ, σ²). Furthermore, assume N and Y are independent.

(b) (10%) Evaluate.

 (Hint: For N, the probability of observing k events is given by P(k events occurring) =)