題組內容
Anscombe(1973)發表了四組數據集,每一組都只有一個解釋變數和一個反 應變數,這四組數據集經常被用來示範散佈圖(scatter plot)在迴歸分析的重 要性。數據如下所示:
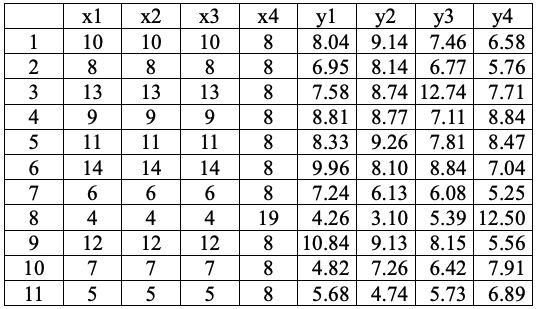
其中「x1, x2, x3, x4」依序分別表示第一組數據集的解釋變數、第二組數據集 的解釋變數、第三組數據集的解釋變數、第四組數據集的解釋變數。「y1, y2, y3, y4」依序分別表示第一組數據集的反應變數、第二組數據集的反應變數、 第三組數據集的反應變數、第四組數據集的反應變數。有了數據之後,在假 設簡單線性迴歸模型之前,通常會先繪製散佈圖,但這一回我們先配適這個 模型「y = A + Bx」,其中「y」是反應變數、「A」是截距、「B」是斜率、「x」 是解釋變數。
答題時,請用「A1」代表第一組數據集上述模型「A」的估計值、「B1」代表 第一組數據集上述模型「B」的估計值;用「A2」代表第二組數據集上述模 型「A」的估計值、「B2」代表第二組數據集上述模型「B」的估計值;用「A3」 代表第三組數據集上述模型「A」的估計值、「B3」代表第三組數據集上述模 型「B」的估計值;用「A4」代表第四組數據集上述模型「A」的估計值、「B4」 代表第四組數據集上述模型「B」的估計值。
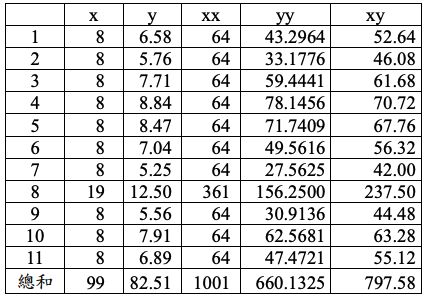
為了估計「A(截距)」和「B(斜率)」,有下列4組數據集。(請注意,欄位 名稱x和y是原始數據、xx表示解釋變數的平方、yy表示反應變數的平方、xy 表示解釋變數乘以反應變數。「總和」為其上方11個數字的加總)
1.第一組數據集:
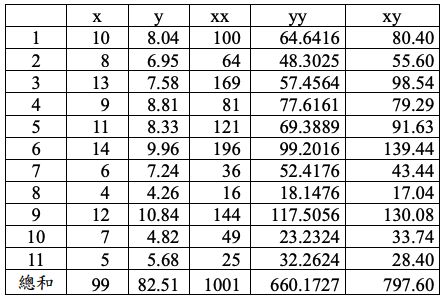
2.第二組數據集:
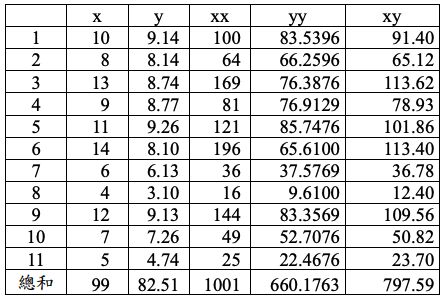
3.第三組數據集:
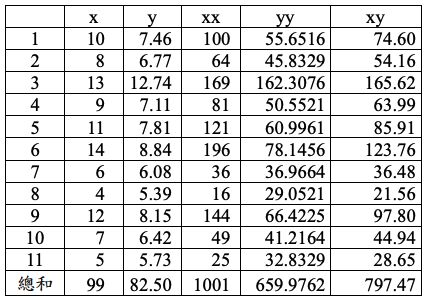
4.第四組數據集: