題組內容

二、將底下的權重無向圖（WeightedUndirectedGraph）用Kruskal演算法建立其最小生成樹（MinimumSpanningTree,MST）。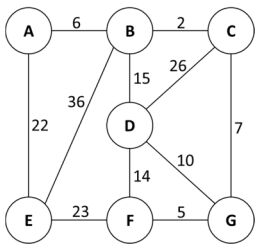
655d593de8f41.jpg

(一)請逐步畫出MST建立的過程。（12分）

詳解 (共 1 筆)

詳解 提供者：hchungw

要使用 Kruskal 的演算法來找出給定的加權無向圖的最小生成樹（MST），我們將按照以下步驟操作：

  1. 排序邊：將所有的邊按照權重從小到大排序。
  2. 初始化森林：將圖中的每個頂點初始化為一個單獨的樹，即森林的每一棵樹只包含一個節點。
  3. 選擇邊：從權重最小的邊開始，如果這條邊連接的兩個頂點屬於不同的樹，則添加這條邊到我們的MST中，並合併這兩棵樹。如果這條邊連接的兩個頂點已經在同一棵樹中，則忽略這條邊，以避免形成循環。
  4. 重複選擇：重複步驟3，直到森林變成一棵樹，即MST包含了所有的頂點。

根據您提供的圖，邊的權重已經標明。我會開始執行 Kruskal 的演算法來找出 MST。請稍等，我將為您完成這個過程。

 

使用 Kruskal 的演算法，我們可以找到給定無向加權圖的最小生成樹，其邊和總權重如下：

  1. 邊 B−C 有權重 2
  2. 邊 F−G 有權重 5
  3. 邊 A−B 有權重 6
  4. 邊 C−G 有權重 7
  5. 邊 D−G 有權重 10
  6. 邊 A−E 有權重 22

這些邊組成了最小生成樹，總權重是 52。