題組內容
一、假設算術運算元(Operator)的優先次序(Precedence)與結合性 (Associativity)如下: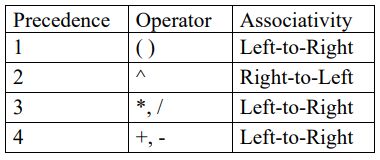
給定中序(Infix)運算式:x - y /(6 * z)+ 8 * p ^ q ^ r
(二)寫出它的前序(Prefix)運算式。(10分)
詳解 (共 1 筆)
詳解
將中序運算式 x - y / (6 * z) + 8 * p ^ q ^ r 轉換為前序(Prefix)運算式的步驟與後序類似,但運算符的處理順序會有所不同。這次我們從運算式的最右邊開始向左處理,並將運算符放在其運算數之前。以下是轉換過程:
以相反的順序掃描中序運算式(從右至左)。
遇到操作數 x,y,6,z,8,p,q,r 時,將其放入輸出。
對於運算符,如果它的優先級高於棧頂的運算符,或者它具有右至左的結合性且優先級等於棧頂的運算符,則將其壓入棧。
如果當前運算符的優先級低於棧頂的運算符,或者具有左至右結合性且優先級等於棧頂的運算符,則將棧頂的運算符彈出並放入輸出,直到遇到一個優先級更低的運算符為止,然後將當前運算符壓入棧。
遇到右括號時,將其壓入棧。
遇到左括號時,將棧中的運算符彈出並放入輸出,直到遇到右括號為止,括號不輸出。
按照這個過程,我們可以得到中序運算式 x - y / (6 * z) + 8 * p ^ q ^ r 對應的前序運算式是:
遇到操作數 x,y,6,z,8,p,q,r 時,將其放入輸出。
對於運算符,如果它的優先級高於棧頂的運算符,或者它具有右至左的結合性且優先級等於棧頂的運算符,則將其壓入棧。
如果當前運算符的優先級低於棧頂的運算符,或者具有左至右結合性且優先級等於棧頂的運算符,則將棧頂的運算符彈出並放入輸出,直到遇到一個優先級更低的運算符為止,然後將當前運算符壓入棧。
遇到右括號時,將其壓入棧。
遇到左括號時,將棧中的運算符彈出並放入輸出,直到遇到右括號為止,括號不輸出。
按照這個過程,我們可以得到中序運算式 x - y / (6 * z) + 8 * p ^ q ^ r 對應的前序運算式是:
+ - x / y * 6 z * 8 ^ p ^ q r
在前序表示法中,運算符位於其對應的運算數之前,與後序表示法剛好相反。