申論題

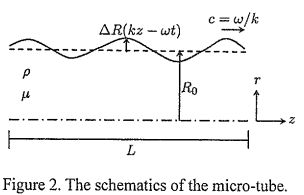
1.(50%) Lymphangions(淋巴管節),functional units of a lymph vessel(淋巴管)that lie between two semilunar values (瓣膜), are muscular and capable of contracting themself one by one to propel the lymph(淋巴液) forward and increase the fluid pressure (figure 1). A lymph vessel now is modeled by a micro-tube with a deformable wall as shown in figure 2. The micro-tube has a fixed length L and a radius R₀ when the wall is undeformed. We assume that a lymph vessel is very thin, Ie., R₀ ＜＜ L. We model the operations of lymphangions as a wall deformation in a form of traveling wave, i.e, △R = △R(kz - ωt), where z is the streamwise coordinate, k and ωare wavenumber and angular velocity of the traveling wave, whose traveling velocity is c = ω/k. Thus, the deformable wall is described by an axisymmetric surface at r = R(z, t) = R₀ + △R(kz - ωt). Consider the flow of lymph in the micro-channel is incompressible, axisymmetric and without swirling. The lymph is assumed to have constant densityρ and dynamics viscosity μ.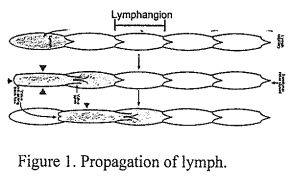 

The following incompressible axisymmetric no-swirling Navier-Stokes equations in the cylindrical coordinate will be helpful:
   where p is the pressure and up and uz are the radial and streamwise components of velocity.

(6) (10%) Since R(z, t) is in a form of a traveling wave, A(z,t) and Q(z,t) are too in a form of traveling wave. From the results in part (d) show that Q(z,t) = cA(z,t) + Q₀(t) . Together with the results from part (e), derive an expression of the pressure gradient in the z direction in terms of Q₀(t), R0, △R, c, andμ.