題組內容
一、假設有一個記錄某產品尺寸(如:公厘)的管制圖(如圖一),其中 x 軸是時間,y
軸是尺寸,y 軸上有中心線(central limit, CL)為μ0, μ0 + 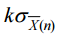 為上界限(upper
limit, UL), μ0 −
為上界限(upper
limit, UL), μ0 −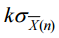 為下界限(lower limit, LL)。品管工程師每 h 小時抽檢一次,
每一次抽出 n 個產品,量測出該 n 個產品尺寸 X1, X2, ..., Xn,再將其樣本平均數
X(n)點在管制圖一上。如果樣本平均數
為下界限(lower limit, LL)。品管工程師每 h 小時抽檢一次,
每一次抽出 n 個產品,量測出該 n 個產品尺寸 X1, X2, ..., Xn,再將其樣本平均數
X(n)點在管制圖一上。如果樣本平均數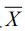 落在上下界限外,則宣告製程有問題(如:
平均數偏移),停止生產,並找尋製程偏移原因(或稱可歸屬的原因)。
落在上下界限外,則宣告製程有問題(如:
平均數偏移),停止生產,並找尋製程偏移原因(或稱可歸屬的原因)。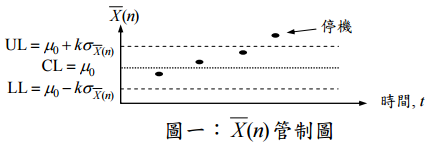
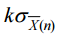 為上界限(upper
limit, UL), μ0 −
為上界限(upper
limit, UL), μ0 −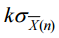 為下界限(lower limit, LL)。品管工程師每 h 小時抽檢一次,
每一次抽出 n 個產品,量測出該 n 個產品尺寸 X1, X2, ..., Xn,再將其樣本平均數
X(n)點在管制圖一上。如果樣本平均數
為下界限(lower limit, LL)。品管工程師每 h 小時抽檢一次,
每一次抽出 n 個產品,量測出該 n 個產品尺寸 X1, X2, ..., Xn,再將其樣本平均數
X(n)點在管制圖一上。如果樣本平均數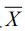 落在上下界限外,則宣告製程有問題(如:
平均數偏移),停止生產,並找尋製程偏移原因(或稱可歸屬的原因)。
落在上下界限外,則宣告製程有問題(如:
平均數偏移),停止生產,並找尋製程偏移原因(或稱可歸屬的原因)。
在本題中之假設條件如下:
i. 假設 X1, X2, ..., Xn獨立(independent)
ii. 假設製程正常時,產品尺寸的平均數 E(X) = μ0 ;而製程偏移後,產品尺寸的平
均數 E(X) = μ0 +δσ0
iii. 製程正常或偏移,產品尺寸的變異數皆為 var(X) =σ02
iv. 假設中央極限定理適用(亦即![]()
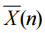 服從常態分配)。求算當 k = 3, n = 16, μ0 = 10,
σ 0 = 0.2, δ = 1 時
v. 令 α 表示製程正常時,
服從常態分配)。求算當 k = 3, n = 16, μ0 = 10,
σ 0 = 0.2, δ = 1 時
v. 令 α 表示製程正常時, 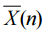 落在上下界限外的機率
vi. β 表示製程偏移後,
落在上下界限外的機率
vi. β 表示製程偏移後,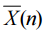 落在上下界限內的機率
問題:
落在上下界限內的機率
問題:
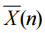 服從常態分配)。求算當 k = 3, n = 16, μ0 = 10,
σ 0 = 0.2, δ = 1 時
v. 令 α 表示製程正常時,
服從常態分配)。求算當 k = 3, n = 16, μ0 = 10,
σ 0 = 0.2, δ = 1 時
v. 令 α 表示製程正常時, 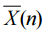 落在上下界限外的機率
vi. β 表示製程偏移後,
落在上下界限外的機率
vi. β 表示製程偏移後,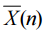 落在上下界限內的機率
問題:
落在上下界限內的機率
問題: