申論題

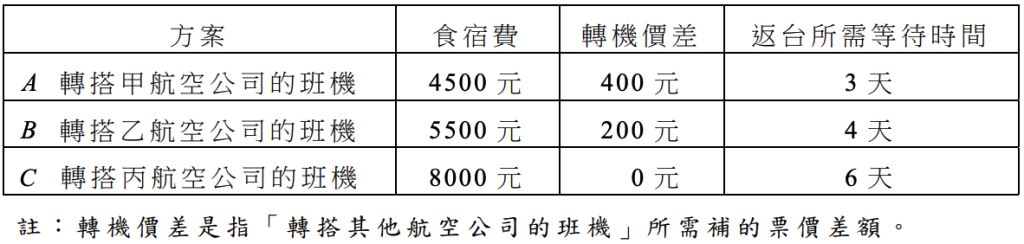方案食宿費轉機價差返台所需等待時間領隊向旅行社報告後，旅行社同意領隊可以使用下列經費來解決此事件：食宿費總共最多 150000 元，轉搭其他航空公司班機的轉機價差總共最多 8000 元 。試問在經費允許的條件下，要如何分配採用 A、 B、 C 這三種方案的人數，才能使全部旅客返回台灣所用的等待總人天數最少？所謂等待總人天數是採用各方案的人數乘以等待的天數之總和，例如：若採用A、 B、C方案的人數分別為 8、10、7 人，則等待總人天數為 8x3+10x4+7x6=106（人天）。如果領隊規劃 x 人轉搭甲航空公司的班機、y人轉搭乙航空公司的班機，其餘的旅客轉搭丙航空公司的班機，由下列步驟，求出全部旅客返回台灣所用的最少等待總人天數。